Pure Pursuit Problem Code - Matlab and C code of Pure pursuit problem

Pure Pursuit Problem Code - Matlab and C code of Pure pursuit problem

What is Pure pursuit:

Pure pursuit is a type of pursuit curve used in aerial combat in which an aircraft pursues another aircraft by pointing its nose directly towards it.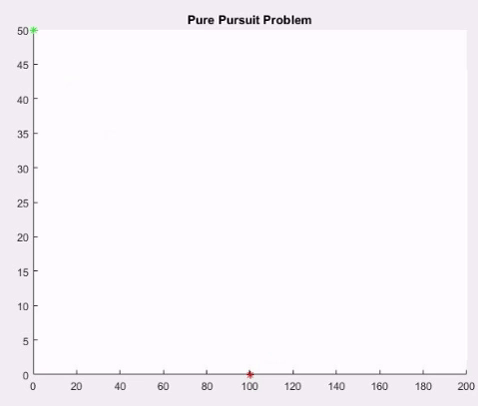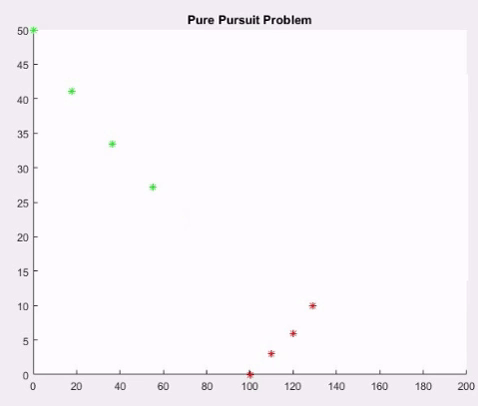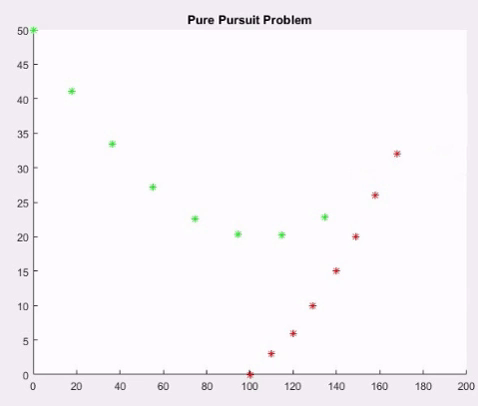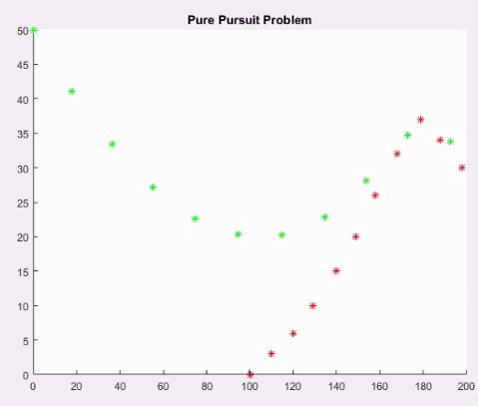

What is mainly Pure pursuit is:

Logic Behind the pure pursuit problem of simulation:

1. Bomber Aircraft and a Fighter Aircraft are flying in the a horizontal plane. 
2. Fighter aircraft and bomber aircraft both are moving inside the rectangular range.  
3. The fighters and bombers have a velocity given, suppose s = 20 in our code.
4. When the distance of the Bomber and the Fighter is less than 12 units, it is assumed that the Bomber is shot down or destroyed.
5. The distance between this the bombers and fighter follows the distance rule - dist[t] = √( (yb[t]-yf[t])² + (xb[t]-yf[t])² ). 
6. In matlab the distance will be dist = sqrt(y^2+x^2). 
7. Look the pure pursuit problem code now and hope it'll clear to you.

Pure Pursuit Problem MatLab Code

clc;
hold all;
xb=[100 110 120 129 140 149 158 168 179 188 198 209 219 226 234 240];
yb=[0 3 6 10 15 20 26 32 37 34 30 27 23 19 16 14];

xf = [];
yf = [];
xf(1)=0;
yf(1)=50;
s=20;
dist=0;

for i=1:15
   pause on;
    plot(xb(i),yb(i),'r*');
    title('Pure Pursuit Problem');
    pause(1);
    plot(xf(i),yf(i),'g*');
    y=yb(i)-yf(i);
    x=xb(i)-xf(i);
    
  dist=sqrt(y^2+x^2);

  if(dist<=12)
        fprintf('Bomber destroyed at  %d s',i);
        break;
  end
  
  xf(i+1)=xf(i)+s*((xb(i)-xf(i))/dist);
  yf(i+1)=yf(i)+s*((yb(i)-yf(i))/dist);
end

Pure Pursuit Problem Output - Matlab:

Pure Pursuit problem in C language:

Code:

#include < stdio.h >
#include < math.h >
#include < stdlib.h >

void main()
  {
   float xf,yf, xb,yb,d,distance;
   int flag=0,
   vf=20,
   time=0;
   randomize();
   xf=rand()%1001;
   yf=rand()%1001;
   xb=rand()%1001;
   yb=rand()%1001;
   while(flag==0)
    {
 d= (yb-yf)*(yb-yf)+(xb-xf)*(xb-xf);
 distance=sqrt(d);
 printf("time=%d   xf=%5.2f  yf=%5.2f  xb=%5.2f  yb=%5.2f  distance=%5.2f\n\n",time,xf,yf,xb,yb,distance);
 if(distance >100)
   {
    printf("The bomber plain was shot down at %d second\n",time);
    flag=1;
   }
 else if(distance>900)
   {
     printf("The bomber plane escaped from sight at %d second\n", time);
     flag=1;
   }
 else
   {
     xf=xf+vf*(xb-xf)/distance;
     yf=yf+vf*(yb-yf)/distance;
     xb=rand()%1001;
     yb=rand()%1001;
     time=time+1;
   }
    }
    getch();
}

Output C code Pure Pursuit:

CASE 1:  BOMBER  IS SHOT DOWN BY FIGHTER

time=0   xf=688.00  yf=796.00  xb=366.00  yb=119.00  distance=749.68

time=1   xf=679.41  yf=777.94  xb=563.00  yb=771.00  distance=116.62

time=2   xf=659.45  yf=776.75  xb=419.00  yb=939.00  distance=290.07

time=3   xf=642.87  yf=787.94  xb=87.00  yb=931.00  distance=573.98

time=4   xf=623.50  yf=792.92  xb=960.00  yb=247.00  distance=641.30

time=5   xf=633.99  yf=775.90  xb=197.00  yb=203.00  distance=720.54

time=6   xf=621.86  yf=759.99  xb=799.00  yb=891.00  distance=220.32

time=7   xf=637.94  yf=771.89  xb=207.00  yb=310.00  distance=631.70

time=8   xf=624.30  yf=757.26  xb=193.00  yb=915.00  distance=459.24

time=9   xf=605.52  yf=764.13  xb=311.00  yb=991.00  distance=371.76

time=10   xf=589.67  yf=776.34  xb=816.00  yb=304.00  distance=523.76

time=11   xf=598.31  yf=758.30  xb=804.00  yb=587.00  distance=267.68

time=12   xf=613.68  yf=745.50  xb=122.00  yb=530.00  distance=536.84

time=13   xf=595.36  yf=737.47  xb=924.00  yb=705.00  distance=330.24

time=14   xf=615.27  yf=735.51  xb=100.00  yb=508.00  distance=563.26

time=15   xf=596.97  yf=727.43  xb=48.00  yb=39.00  distance=880.51

time=16   xf=584.50  yf=711.79  xb=990.00  yb=710.00  distance=405.50

time=17   xf=604.50  yf=711.70  xb=523.00  yb=629.00  distance=116.11

time=18   xf=590.46  yf=697.46  xb=894.00  yb=148.00  distance=627.72

time=19   xf=600.13  yf=679.95  xb=463.00  yb=537.00  distance=198.09

time=20   xf=586.29  yf=665.52  xb=308.00  yb=709.00  distance=281.67

time=21   xf=566.53  yf=668.61  xb=488.00  yb=605.00  distance=101.06

time=22   xf=550.99  yf=656.02  xb=107.00  yb=522.00  distance=463.77

time=23   xf=531.84  yf=650.24  xb=305.00  yb=777.00  distance=259.86

time=24   xf=514.38  yf=659.99  xb=250.00  yb=794.00  distance=296.40

time=25   xf=496.54  yf=669.04  xb=448.00  yb=950.00  distance=285.13

time=26   xf=493.14  yf=688.74  xb=252.00  yb=285.00  distance=470.27

time=27   xf=482.88  yf=671.57  xb=623.00  yb=646.00  distance=142.43

time=28   xf=502.56  yf=667.98  xb=640.00  yb=327.00  distance=367.64

time=29   xf=510.03  yf=649.43  xb=357.00  yb=811.00  distance=222.54

time=30   xf=496.28  yf=663.95  xb=623.00  yb=353.00  distance=335.78

time=31   xf=503.83  yf=645.43  xb=156.00  yb=371.00  distance=443.06

time=32   xf=488.13  yf=633.04  xb=533.00  yb=117.00  distance=517.99

time=33   xf=489.86  yf=613.12  xb=301.00  yb=627.00  distance=189.37

time=34   xf=469.91  yf=614.59  xb=143.00  yb=263.00  distance=480.09

time=35   xf=456.29  yf=599.94  xb=780.00  yb=654.00  distance=328.19

time=36   xf=476.02  yf=603.23  xb=928.00  yb=422.00  distance=486.96

time=37   xf=494.58  yf=595.79  xb=757.00  yb=44.00  distance=611.01

time=38   xf=503.17  yf=577.73  xb=734.00  yb=192.00  distance=449.52

time=39   xf=513.44  yf=560.57  xb=49.00  yb=949.00  distance=605.47

time=40   xf=498.10  yf=573.40  xb=515.00  yb=893.00  distance=320.05

time=41   xf=499.16  yf=593.37  xb=111.00  yb=765.00  distance=424.41

time=42   xf=480.87  yf=601.46  xb=463.00  yb=633.00  distance=36.25

The bomber plain was shot down at 42 second

CASE 2: BOMBER  ESCAPES FROM  THE SIGHT OF FIGHTER

time=0   xf=642.00  yf=902.00  xb=788.00  yb=709.00  distance=242.00

time=1   xf=654.07  yf=886.05  xb=585.00  yb=997.00  distance=130.69

time=2   xf=643.50  yf=903.03  xb=587.00  yb= 6.00  distance=898.81

time=3   xf=642.24  yf=883.07  xb=11.00  yb=162.00  distance=958.33

The bomber plane escaped from sight at 3 second

Links Where you can learn more on Pure pursuit problem:

1. Wikipedia - Pure Pursuit
2. Mathworks - Pure Pursuit

Tags:

Pure Pursuit Problem Code - Matlab and C code of Pure pursuit problem, Pure pursuit problem, Pure pursuit problem code, pure pursuit solution in c language, pure pursuit simulation, pure pursuit logic, pure pursuit algorithm, pure pursuit learning, pure pursuit explanation,